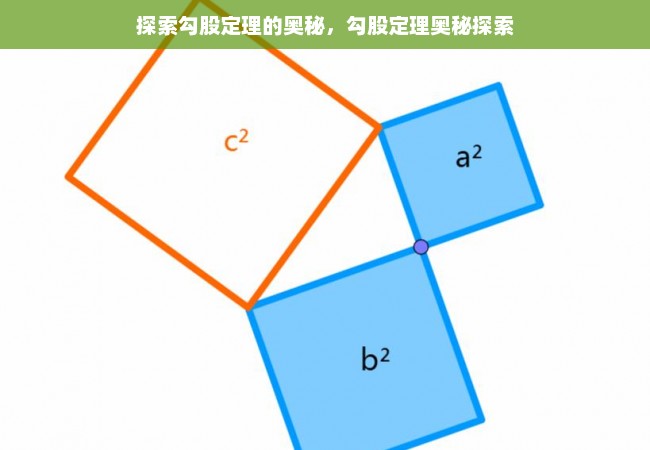
一、勾股定理的历史渊源
勾股定理是一个古老而重要的数学定理,它在数学的发展历程中占据着重要的地位,在中国古代,直角三角形被称为勾股形,早在公元前十一世纪,周朝数学家商高就提出了“勾三股四弦五”的特例,而在西方,毕达哥拉斯学派也对勾股定理有着深入的研究和证明。
勾股定理的证明方法众多,其中一种常见的方法是拼图法,我们可以用四个完全相同的直角三角形(直角边为 a 和 b,斜边为 c)拼成一个边长为(a+b)的正方形,通过计算大正方形的面积,可以得到:(a+b)² = 4×(1/2)ab + c²,化简后即可得到 a² + b² = c²,从而证明了勾股定理。
二、勾股定理在几何中的应用
勾股定理在几何中有着广泛的应用,它可以帮助我们解决许多与直角三角形相关的问题,已知直角三角形的两条直角边,可以利用勾股定理求出斜边的长度;或者已知斜边和一条直角边,求出另一条直角边。
证明勾股定理的另一种方法是赵爽弦图法,赵爽是中国古代著名的数学家,他通过构造弦图来证明勾股定理,弦图是由四个直角三角形和一个小正方形组成的大正方形,通过对弦图中各部分面积的计算和分析,可以巧妙地证明勾股定理。
三、勾股定理与代数的联系
勾股定理不仅仅局限于几何领域,它与代数也有着紧密的联系,在代数中,我们可以通过方程的形式来表达勾股定理,对于一个直角三角形,设其两条直角边分别为 x 和 y,斜边为 z,则可以得到方程 x² + y² = z²。
还有一种证明勾股定理的方法是相似三角形法,通过构造两个相似的直角三角形,利用相似三角形的性质,可以得到对应的边之间的比例关系,进而证明勾股定理。
四、勾股定理的拓展与延伸
勾股定理在数学中有着广泛的拓展和延伸,在三维空间中,也存在着类似勾股定理的关系,即长方体的对角线长度的平方等于长、宽、高的平方和,勾股定理还与三角函数等其他数学概念有着密切的联系。
证明勾股定理的另一种有趣的方法是总统证法,据说这是美国第 20 任总统加菲尔德发现的一种证明方法,他利用梯形的面积公式,通过巧妙的计算和推理,证明了勾股定理。
五、勾股定理的深远影响
勾股定理的影响不仅仅局限于数学领域,它还在物理学、工程学、计算机科学等诸多领域中发挥着重要的作用,它为我们提供了一种解决实际问题的有力工具,帮助我们更好地理解和探索世界。
勾股定理是数学中的一颗璀璨明珠,它的证明方法多样,应用广泛,通过对勾股定理的深入研究和探索,我们可以更好地领略数学的魅力和奥秘,同时也为我们解决实际问题提供了更多的思路和方法,无论是在古代还是现代,勾股定理都将继续发挥着重要的作用,引领着我们在数学的海洋中不断前行。
文章仅供参考,你可以根据实际情况进行调整和修改,如果你还有其他问题,欢迎继续向我提问,我会尽力为你提供帮助。